机器学习概览(上)
这个系列的文章我们主要讲解机器学习与数据挖掘领域最常用的一些算法,具体包括有监督学习的分类与回归算法以及无监督学习的聚类算法,一共分为(上)和(下)两篇。这里先介绍上篇的相关内容。
1. K-Nearest Neighbor(K近邻算法)
k近邻(K-Nearest Neighbor,K-NN)算法是在1968年由Cover和Hart提出,是一种基本的分类和回归方法。本文这里只讨论关于分类问题的k近邻法。k近邻算法的输入为实例的特征向量,对应于特征空间的点;输出为实例的类别,可以取多类。其算法原理为:给定一个训练数据集,其中现有的实例数据类别已定,对新的输入实例,在训练数据集中找到与该实例最邻近的K个实例,这K个实例的多数属于某个类,就把该输入实例分类到这个类中。下面让我们先从一个实际的例子来从直观上了解一下什么是K-近邻算法。

如上图所示,现在有两类不同的样本数据,分别用蓝色的小正方形和红色的小三角形表示,而图正中间的那个绿色的圆所表示的数据则是待分类的未知数据。这也就是我们的目的,来了一个新的数据点,我要得到它的类别是什么?下面我们根据k近邻算法的思想来给绿色圆点进行分类。
- 如果
K = 3,距离绿色圆点最邻近的3个点分别是2个红色小三角形和1个蓝色小正方形,根据少数服从多数的原则,基于统计的方法,判定绿色的这个待分类点属于红色的三角形一类。 - 如果
K = 5,距离绿色圆点最邻近的5个点分别是是2个红色三角形和3个蓝色的正方形,根据少数服从多数的原则,基于统计的方法,判定绿色的这个待分类点属于蓝色的正方形一类。
好了,通过上面的这个例子,相信已经让你对KNN算法有了一个比较直观的认识,下面就让我们来正式揭开K近邻算法的神秘面纱,这里将从以下几个方面来分别进行介绍。
1.1 一些前置假设
- 训练集:
- 输入空间:
(其中,
表示为实例的特征向量,
表示为
维实数向量空间,
)
- 输出空间:
(其中,
表示为实例所属的类别,
)
1.2 K近邻算法基本思想
K近邻算法并不具有显式的学习过程,K近邻算法实际上是利用训练集数据对特征空间进行划分,并作为其分类的模型。给定一个训练集,对于新的输入实例,首先在训练集中找到与该实例最近的K个实例,然后统计这K个实例的多数属于哪个类别,就把该实例划分为哪个类别。
1.3 K近邻算法的三个要素
经过上面的分析,我们可以总结出K近邻算法的三个基本要素,它们分别为:
- K值的选择
- 距离的度量
- 分类决策的准则
在k近邻算法中,当训练集、距离度量(如欧氏距离)、k值以及分类决策准则(如多数表决)确定后,对于任意一个新的输入实例,它所属的类别也被唯一的确定。这相当于根据上述要素将特征空间划分为一些子空间,确定子空间里的每个点所对应属于的类别。
下面就来对这三个基本要素进行一一的详细介绍。
1.3.1 K值的选择
K值的选择会对k近邻算法的结果产生重大的影响。
首先考虑一个极端的情况,当K值为1时,此时的K近邻算法又称为最近邻算法,这种情况下,很容易发生过拟合,很容易将一些噪声学习到模型中(很容易将实例判定为噪声类别)。即如果选择较小的K值,相当于用较小的邻域中的训练实例进行预测,意味着整体模型变得复杂,因而容易产生过拟合。
我们再考虑另外一种极端情况,当K值为N时,此时不管你输入的实例是什么类别,最终的模型都会将该实例判定为模型中实例最多的类别。也就是在这种情况下,很容易发生欠拟合。即如果选择较大的K值,相当于用较大的邻域中的训练实例进行预测,但是这个时候距离输入实例较远的训练实例点也会对结果产生影响,容易使得预测发生偏差,意味着整体模型变得简单,容易发生欠拟合。
因此,K值的选择既不能过大,也不能过小(似乎说了一句废话hhh)。那么我们一般怎么选取呢?在李航博士的《统计学习方法》这本书上讲到,我们一般选取一个较小的数值,而且通常采取交叉验证法来选取最优的k值。(即:选取K值很重要的关键是实验调参,类似于神经网络需要多少个隐层这种,通过调整超参数来得到一个相对较好的结果)。
1.3.2 距离的度量
在机器学习领域,常见的距离度量方法有以下四种,分别为:
- 闵可夫斯基距离
- 曼哈顿距离
- 欧氏距离
- 切比雪夫距离
下面分别对这四种距离的计算公式进行简单的介绍。
假设有两个特征向量(其中,与
的定义与前面一致,这里不再重复说明):
那么向量与向量
之间的闵可夫斯基距离的定义如下:
注意:这里的。
当 p = 1 时就是曼哈顿距离(Manhattan distance),其具体的公式为:
当 p = 2 时就是欧氏距离(Euclidean distance),其具体的公式为:
当 p = 时就是切比雪夫距离,亦即各个坐标距离的最大值,其数学表达式为:
一般情况下,在特征空间中两个实例点的距离是两个实例点相似程度的反映。在实际应用中,距离函数的选择应该根据当前数据的特性和分析的需要而确定,对于k近邻算法模型,一般选取p = 2的欧式距离来表示,但是也可以用其他距离,比如更一般的闵可夫斯基距离。
1.3.3 分类决策的准则
这利用的是多数表决的决策准则,即由输入实例的个邻近的训练实例的多数类决定输入实例的类。
多数表决规则(majority voting rule)有如下解释:如果分类的损失函数为0-1损失函数,分类函数为:
那么误分类的概率为:
对于给定的实例,其最邻近的
个训练实例点构成的集合
。如果涵盖
的区域的类别是
,那么误分类的概率是:
要使得误分类率最小即经验风险最小,就要使得最大,所以多数表决规则等价于经验风险最小化。
1.4 特征归一化
为了让各个特征在分类的时候同等重要,亦即消除不同特征的量纲对于模型最后结果的影响,因此,特征归一化的主要作用是同一量纲。因为如果特征的量纲不同,在进行距离的计算时(比如欧氏距离),量纲越大的特征对最后结果的影响也就越大,最终的结果也会偏向于量纲比较大的特征。综上原因,我们需要将各个特征进行归一化。
常用的数据归一化方法有两种,下面分别来简单进行介绍一下:
- 最值归一化(线性归一化)
所谓最值归一化,即:把所有的数据都映射到之间。
这种归一化方法比较适用在数值比较集中的情况。这种方法有个缺陷,如果和
不稳定,很容易使得归一化结果不稳定,使得后续使用效果也不稳定。实际使用中可以用经验常量值来替代max和min。(该方法使用于数据集存在明显的边界,有最大值和最小值的情况)
- 均值方差归一化(标准化)
所谓均值方差归一化,即:把所有的数据归一到均值为方差为
的分布中。
1.5 对异常值不敏感
由于KNN是基于距离的算法,所以KNN对异常值是不敏感的(这里面提到的异常值,简单来说,即在数据集中存在不合理的值,又称离群点)。
1.6 KNN模型算法流程&&代码详解
这一节我们讲述k近邻算法的流程以及python代码实现。首先我们来看看K近邻算法的流程步骤,它主要可以分为两大步:
(1) 根据给定的距离度量,在训练集中找出与
最邻近的
个点,涵盖这
个点的
的邻域记为
;
(2) 在中根据分类决策准则(如多数表决)决定
的类别
:
在上面的公式中,为指示函数,即当
时,
为1,否则
为0。
以上就是k近邻算法的主要流程,下面介绍k近邻算法的python代码实现。
from sklearn.datasets import load_iris
import numpy as np
# 从sklearn中导入iris数据集
iris = load_iris()
X = iris.data
y = iris.target
# 计算data1和data2的欧几里得距离。
def euclideanDistance(data1, data2):
distance = 0
# data1和data2长度一致,这里我们就使用data1的长度
for x in range(len(data1)):
distance += np.square(data1[x]-data2[x])
return np.sqrt(distance)
# 定义KNN模型
def KNN(X, y, testInstance, k):
distances = dict()
# 为了得到测试数据的预测类别,对训练集每条数据进行迭代
for idx, trainInstance in enumerate(X):
# 1. 计算测试数据与训练集中每一条数据的距离。
dist = euclideanDistance(testInstance, trainInstance)
distances[idx] = dist
#2. 对距离进行升序排列
sorted_d = sorted(distances.items(), key=lambda k:k[1])
neighbors = []
#3. 对排列结果选择前K个值
for x in range(k):
neighbors.append(sorted_d[x][0])
classVotes = dict()
#4. 得到出现次数最多的类
for x in range(len(neighbors)):
label = y[neighbors[x]]
if label in classVotes:
classVotes[label]+=1
else:
classVotes[label]=1
#5. 返回测试数据的预测类别
sortedVotes = sorted(classVotes.items(), key=lambda k:k[1], reverse=True)
return (sortedVotes[0][0], neighbors) 1.6.1 测试代码&&结果展示
testInstance = [7.2, 3.6, 5.1, 2.5]
# K值为1
k = 1
predicted, neighbors = KNN(X, y, testInstance, k)
print('predicted:',predicted)
print('neighbors:',neighbors)
运行结果
predicted: 2
neighbors: [141]
# K值为3时
k = 3
predicted, neighbors = KNN(X, y, testInstance, k)
print('predicted:',predicted)
print('neighbors:',neighbors)
运行结果
predicted: 2
neighbors: [141, 139, 120]
# K值为5时
k = 5
predicted, neighbors = KNN(X, y, testInstance, k)
print('predicted:',predicted)
print('neighbors:',neighbors)
运行结果
predicted: 2
neighbors: [141, 139, 120, 145, 144] 1.7 KNN算法的优缺点
在本节的最后,来说一下K近邻算法的优点和缺点。
优点:
- 理论成熟,思想简单,既可以用来做分类又可以做回归
- 可以用于非线性分类
- 计算精度高(计算距离)
- 对异常值不敏感(单纯根据距离进行分类)
- 无数据输入假定(不会对数据预先进行判定)
缺点:
- 计算量大,尤其是特征数非常多的时候,因而会容易导致时间复杂度高,空间复杂度高
- 样本不平衡的时候,对稀有类别的预测准确率低
- 是惰性学习方法,基本上不学习,导致预测时速度比起逻辑回归之类的算法慢
- 模型可解释性不强
适用数据范围:数值型和标称型
2. Linear Regression(线性回归)
回归是统计学里面最常用的算法之一,线性回归是指最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。要想搞清楚什么是线性回归,首先我们得搞清楚两个概念,即什么是线性?什么是回归?
所谓线性,就是说两个变量之间的关系是一次函数关系,即画出来的函数图像是一条直线,称之为线性。但是由一点需要注意,线性回归里面的线性指的是广义的线性,即数据与数据之间的关系。
所谓回归,是相对分类来讲的。机器学习的算法目前业界普遍认为是分为三类:监督学习、无监督学习以及半监督学习(也有称作为强化学习)。在这其中,监督学习算法可以分为两大类,分别就指的是分类算法与回归算法,它们之间的区别就是根据类别标签分布类型为离散型、连续性而定义的。回归算法用于连续型分布预测,针对的是数值型的样本,使用回归算法模型,可以在给定输入的时候预测出一个数值,这是对分类方法的提升,因为这样可以预测连续型数据而不仅仅是离散的类别标签。
以上是关于线性回归的简单介绍,线性回归的实际应用在我们的日常生活中有很多,譬如根据历史的气象信息预测明天的温度、根据历史行情预测明天股票的走势、根据历史记录来预测某篇文章的点击率等都属于回归问题。对大量的观测数据进行处理,从而得到比较符合事物内部规律的数学表达式。也就是说,线性回归的本质是为了寻找到数据与数据之间的规律所在,从而就可以模拟出结果,也就是对结果进行预测。解决的就是通过已知的数据得到未知的结果。下面本文就从以下几个方面来详细的阐述线性回归算法。
2.1 一些定义符号
假设数据集为:{},参数为
,其中:
- 训练样本数目为
- 第 i 个样本为
(
为输入样本实例)
(
为输入样本实例对应的值)
(
表示为特征样本的参数(权重))
2.2 假设函数
线性回归就是能够用一个直线较为精确地描述数据之间的关系,这样当出现新的数据的时候,就能够预测出一个简单的值。其具体的形式形如:
从上面的公式中可以看出,只要我们求出对应的权重系数,就能找到对应的预测函数。但是,这里我们注意下:线性回归得出的模型不一定是一条直线
- 在只有一个变量的时候,模型是平面中的一条直线;
- 有两个变量的时候,模型是空间中的一个平面;
- 有更多变量时,模型将是更高维的。
线性回归模型具有很好的可解释性,可以从权重直接看出每个特征对最终结果的影响程度。线性回归适用于
和
之间存在线性关系的数据集,我们可以使用计算机辅助画出散点图来观察它们之间是否存在线性关系。我们尝试使用一条直线来拟合数据,使所有点到直线的距离之和最小。
2.3 目标函数
2.3.1 目标函数的形式(均方误差)
实际上,线性回归中通常使用残差平方和,即点到直线的平行于y轴的距离而不是用垂线距离,残差平方和除以样本量n得到的就是均方误差。均方误差作为线性回归模型的损失函数(cost function),也称之为目标函数。
$$
2.3.2 为什么要选择这样的目标函数?
(1) 对于每一个样例, 假设预测值和真实值存在以下关系:
其中表示预测值和真实值之间的差值(因为预测值和真实值之间总是存在差异的)。
(2) 影响误差的因素有很多,这些因素又都是随机分布的。根据中心极限定理,许多独立随机变量的和趋于正态分布。因此,误差具有以下的两个特点:一、误差
是独立的并且具有相同的分布(
);二、误差
服从均值为0、方差为
的标准正态分布(也称标准高斯分布)。所以我们可以进一步假设:
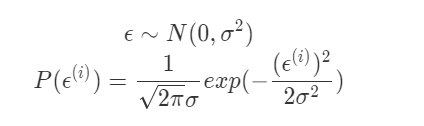
当给定参数和变量
时,联立以上公式,可以得出有以下公式成立:
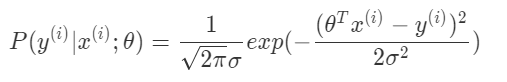
(3) 再进一步假设各个样例的误差是独立同分布的,可以得到对应的似然函数:
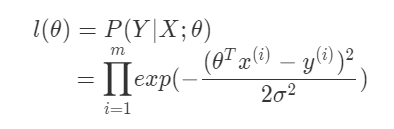
其中,是样本的数量,所以是累乘。因为似然函数表示的是在参数
下数据集出现的概率,所以我们需要做的工作就是极大化似然函数。
(4) 将似然函数转化为对数似然(之所以这样做的原因是:对数运算可以将乘法转换成加法,从而可以简化计算):
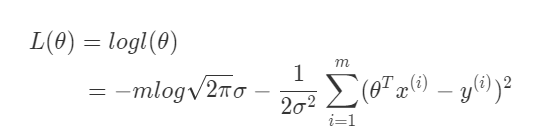
转换为对数似然函数后,需要做的工作也转变为极大化对数似然函数,要极大化对数似然函数,从式子中可以得出,我们的目标是要让让似然函数(单调性相同,对数变换后也一样)越大越好,因此,需要使得的值越小越好。到这一步也基本可以对我们为什么选择这样的目标函数做出一个比较合理的解释了。
2.4 优化目标函数的方法
在得到目标函数的数学形式以及它为什么是这种形式之后,下一步的工作就是来求解它了,目前求解的方法主要有两种,下面一一进行详细介绍。
2.4.1 最小二乘法
对于比较低维的数据,我们可以通过最小二乘法直接求解出对应的解析解形式。具体操作步骤如下:
首先,我们将目标函数展开成向量形式:
对上式求偏导可得:
令其偏导数等于0,可得:
$$
对应于给定样本的数据(已知),一般情况下都可求解。并不一定可直接求解,线性回归可以当做是一个特例。
2.4.2 梯度下降算法(Gradient Descent)
在上面最小二乘法的最后也提到了,由于目标函数并不一定可以直接求解。在这里举个例子,假设我们需要优化一个深度神经网络DNN的网络参数(即优化此网络对于已知数据拟合结果的正确性),可不可以用最小二乘准则去求解呢?答案是可以。但是同时,由于DNN模型本身的复杂性,我们没有办法像线性拟合时那样,在理论和公式的层面求出一个最优解,因此在这里需要引入所谓的BP算法(实质上就是梯度下降法)进行参数的迭代求解。
首先来看看梯度下降的一个直观的解释。比如我们在一座大山上的某处位置,由于我们不知道怎么下山,于是决定走一步算一步,也就是在每走到一个位置的时候,求解当前位置的梯度,沿着梯度的负方向,也就是当前最陡峭的位置向下走一步,然后继续求解当前位置梯度,向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去,一直走到觉得我们已经到了山脚。当然这样走下去,有可能我们不能走到山脚,而是到了某一个局部的山峰低处。
从上面的解释可以看出,梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。下面的图例可以帮助我们更直观的感受一下什么是梯度下降法。

和前面一样,首先需要确定我们的目标函数:
以上面举过的下山为例(怎样最快到达山谷的最低点),主要有以下三个步骤:
(1)找到当前最合适的方向;
(2)走一小步(走快了有可能越过最低点);
(3)按照方向(偏导)与步伐(更新量)去更新的参数。
好了,相信上面的例子已经让大家初步知道了梯度下降大概是怎么回事,接下来,我们就来具体的讲述梯度下降算法。梯度下降算法常见的有三种:批量梯度下降、随机梯度下降以及小批量梯度下降。
2.4.2.1 批量梯度下降法(Batch Gradient Descent, BGD)
批量梯度下降法,是梯度下降法最常用的形式,具体做法也就是在更新参数时使用所有的样本来进行更新。其具体的计算公式如下所示:
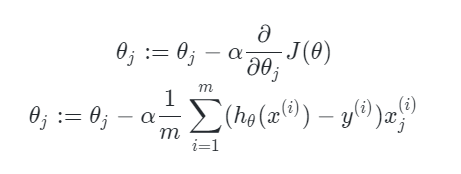
由于我们有个样本,这里求梯度的时候就用了所有
个样本的梯度数据,**上面的
指的是每一步更新梯度所走的步长,也称之为学习率**(后面的
同理)。
批量梯度下降法综合考虑所有样本,容易得到最优解,但是由于每次考虑所有样本,速度很慢。
2.4.2.2 随机梯度下降(Stochastic Gradient Descent, SGD)
随机梯度下降法,其实和批量梯度下降法原理类似,区别在与求梯度时没有用所有的个样本的数据,而是仅仅选取一个样本
来求梯度。当每次只用一个样本训练时,
退化成以下形式:
此时参数更新公式变为以下形式:
随机梯度下降法,和上面提到的批量梯度下降法,是两个极端。一个采用所有数据来梯度下降,一个用一个样本来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说,随机梯度下降法由于每次仅仅采用一个样本来迭代,训练速度很快,而批量梯度下降法在样本量很大的时候,训练速度不能让人满意。对于准确度来说,随机梯度下降法用于仅仅用一个样本决定梯度方向,导致解很有可能不是最优。对于收敛速度来说,由于随机梯度下降法一次迭代一个样本,导致迭代方向变化很大,不能很快的收敛到局部最优解。
那么,有没有一个中庸的办法能够结合两种方法的优点呢?有!这就是下面要讲的的小批量梯度下降法。
2.4.2.3 小批量随机梯度下降(Mini-Batch Gradient Descent, MBGD)
小批量梯度下降法是批量梯度下降法和随机梯度下降法的折中,也就是对于个样本,我们采用
个样本来迭代,其中
。一般可以取
,当然根据样本的数据,可以调整这个
的值。对应的更新公式如下所示:
2.5 线性回归代码详解
def model(theta, X):
"""
预测函数
:param theta: 参数矩阵(nx1)
:param X:输入变量(矩阵mxn)
:return: 输出变量, mx1
"""
return X.dot(theta)
def cost(m, theta, X, y):
"""
代价函数
:param m: 训练集个数
:param theta: 参数矩阵(mx1)
:param X: 输入变量矩阵(mx1)
:param y: 输出变量矩阵(mx1)
:return:
"""
ele = model(theta, X) - y
item = ele ** 2
item_sum = np.sum(item)
return item_sum / (2 * m)
def derivative(m, theta, X, y, n):
"""
对各个theta参数求导(向量形式)
:param m: 训练集个数
:param theta: 参数矩阵(nx1)
:param X: 输入变量矩阵(mxn)
:param y: 输出变量矩阵(mx1)
:param n: 𝜃变量个数𝜃0, 𝜃1, 𝜃2, ..., 𝜃n-1
:return: nx1 矩阵
"""
grad_sum = X.T.dot(model(theta, X) - y)
return grad_sum / m
def gradient(grade_theta, theta, alpha):
"""
𝜃更新
:param grade_theta:求导后的𝜃矩阵(nx1)
:param theta: 更新后的𝜃矩阵(nx1)
:param alpha: 学习率
:return: 返回更新后的𝜃矩阵(nx1)
"""
return theta - alpha * grade_theta
def stop_strage(cost, cost_update, threshold):
"""
停止迭代条件
:param cost:
:param cost_update:
:param threshold:
:return:
"""
return (cost >= cost_update) and (cost - cost_update < threshold)
def linear_regression(X, y):
"""
线性回归模型
:param X: 输入变量矩阵(mxn)
:param y: 输出变量矩阵(mx1)
:param threshold:
:return:
"""
start = time.clock()
m = X.shape[0] # 样本个数
n = X.shape[1]
theta = np.zeros(n).reshape(n, 1) # 设置权重参数的初始值
y = y.reshape(m, 1)
print("theta:", theta.shape, ", X: ", X.shape, "y:", y.shape)
cost_record = [] # 记录代价函数的值
alpha = 0.0001 # 学习率
threshold = 0.01 # 阈值
cost_val = cost(m, theta, X, y)
cost_record.append(cost_val)
iters = 0
while True:
grad = derivative(m, theta, X, y, n)
# 权重参数更新
theta = gradient(grad, theta, alpha)
cost_update = cost(m, theta, X, y)
if stop_strage(cost_val, cost_update, threshold):
break
cost_val = cost_update
cost_record.append(cost_val)
iters += 1
end = time.clock()
print("cost time: %f s" % (end - start))
return cost_record, theta, iters 2.5.1 测试代码&&结果展示
df = pd.read_csv('house_price.csv')
print(df['rooms'].unique())
print(df['halls'].unique())
# 去除脏数据
keep_index = (df['rooms'] != '多') & (df['halls'] != '多')
df = df[keep_index]
# 转换数据类型
df['rooms'] = df['rooms'].astype('int')
df['halls'] = df['halls'].astype('int')
# 截取rooms、halls、size和price
X = df[['rooms', 'halls', 'size']]
y = df['price']
cost_record, theta, iters = linear_regression(X.values, y.values)
print(iters)
print(theta)
print(cost_record)
# 预测数据
# rooms,halls,size,price
# 1,1,49,326
# 2,1,56.45,315
# 2,1,58.3,466
# 3,1,92.33,1061
# 2,1,76.88,408
print model(theta, np.array([1, 1, 49]))
print model(theta, np.array([2, 1, 56.45]))
print model(theta, np.array([2, 1, 58.3]))
print model(theta, np.array([3, 1, 92.33]))
print model(theta, np.array([2, 1, 76.88]))
运行结果:
最终一共迭代iters=11652次,得到的theta=(13.13249986, 12.4409009, 6.59238776)。
[ 338.60040077]
[ 320.84618941]
[ 453.04210675]
[ 1060.51356193]
[ 445.52867125] 2.6 线性回归算法的优缺点
- 优点
- 算法思想简单,实现简洁。建模迅速,对于小数据量、简单的关系非常有效
- 具有良好的可解释性,有利于决策分析
- 是许多强大的非线性模型的基础
- 缺点
- 对于非线性数据或者数据特征间具有多项式回归的难以建模
- 难以很好的表达高度复杂的数据
3. Logistic Regression(LR---逻辑回归)
3.1 引言
看到这个算法的名字,可能大多数之前没接触过机器学习的人会以为LR是回归算法,要是这样想那就大错特错了。逻辑回归处理的是分类问题,线性回归处理的是回归问题。逻辑回归算法是所有机器学习算法里面最简单的,但是简单不代表效果不好。我们在处理机器学习问题时,往往是优先采用简单算法,并对其参数进行优化。如果不能达到你的目的,我们再选择更加复杂的算法如神经网络等。逻辑回归是用来处理分类问题的,其分类边界不一定都是线性的,也可以是非线性的。如下图,一条非线性的决策边界将已有的数据点分成了两类。

上一节我们刚讨论了线性回归算法,知道线性回归得出的是个准确值或区间值,那么我们如何将线性回归算法得到的这个准确值转换为分类值呢?举个例子,高考马上要来临了,我们可以根据你以往的考试成绩对你的高考成绩做一个预测,我们预测的值会是[0,750]中的一个值,但是我想预测下我能否考上大学,那么我就需要将这个回归问题转换为二分类问题。
在这里我们引用一个非常重要的数学函数,sigmod函数。sigmod函数的表达式如下:
接下来,我们直接看sigmod函数的图像。从图像中可以得知,对于任意一个自然数,都可通过sigmod函数将其映射到(0,1)之间的一个值,(0,1)就相当于我们数学中的概率值。我们的二分类问题就是利用概率去判断的,比如判断中国队能否赢下这场比赛,如果预测的概率大于某一个临界值,比如0.6,那我们就可以预测中国队赢。
我们再举高考的例子,线性回归模型预测我得了500分,但不能给出能否考上的结果。这是再使用逻辑回归算法,将分数转换为概率值。假如概率值>0.5,我们就认为能考上,概率值<0.5,我们就认为没有考上。这就是通过逻辑回归算法将回归问题转化为了分类问题。
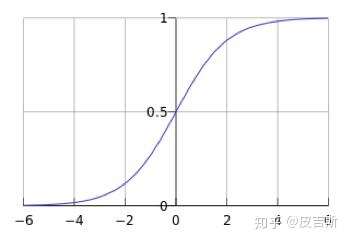
下面我们就来具体讲解一下逻辑回归算法的详细推导以及计算过程。
3.2 推导过程(LR的损失函数与参数更新公式)
假设要解决的问题是一个二分类问题,目标值为{0,1},以线性回归为基础,将模型输出映射到[0,1]之间。我们选择这样一个函数:
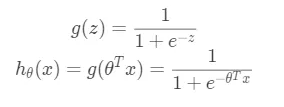
其中被称为sigmoid函数(上面也提到过了)。为什么要选择sigmoid函数其实是可以通过指数分布族加上广义线性模型进行推导分析的。通过sigmoid函数我们可以计算单个样本属于正类还是负类的概率:
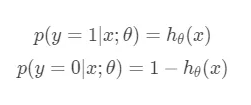
我们将上面两个式子合并成一个:
有了上面这个式子,我们就能很容易的得到函数在在整个数据集上的似然函数:
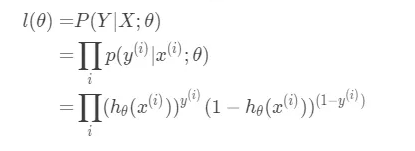
将其转为对数似然函数:
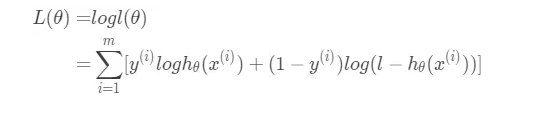
假设我们用随机梯度下降法更新参数,每次只用一个样例,则上面的对数似然函数退化成:
更新参数的公式为:
这里的就是学习率。其次注意式子里面的“+”,因为我们要极大化对数似然函数,所以我们需要沿着梯度方向更新参数。接下来我们要做的就是求出
对各个参数的偏导。
- 首先我们知道sigmoid函数的求导结果为:
- 我们可以推导出
对各个参数的偏导为:
- 所以,参数更新公式为:
如果我们用梯度下降法,每次更新参数用所有样例,则参数更新公式为:
以上即为该算法的推导过程,相对比较简单,但是在各大厂的算法面试过程中会被经常问到要手推,所以逻辑回归的推导最好熟练掌握。
3.3 逻辑回归算法代码详解
逻辑回归算法由于其经典性以及广泛适用性,不过数学推导过程经常在面试中被问到,其具体的代码实现也是面试过程中的热门问题之一,下面即为LR算法的python代码实现。
import numpy as np
import random
# 初始化函数,初始化学习率、迭代的次数。
def __init__(self, learning_rate=.1, n_iterations=4000):
self.learning_rate = learning_rate
self.n_iterations = n_iterations
def initialize_weights(self, n_features):
# 初始化参数
# 参数范围[-1/sqrt(N), 1/sqrt(N)]
limit = np.sqrt(1 / n_features)
w = np.random.uniform(-limit, limit, (n_features, 1))
b = 0
self.w = np.insert(w, 0, b, axis=0)
# sigmoid函数
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# 逻辑回归的主要核心函数,X加多一列全1的值,这样wx相当于wx + b。然后根据迭代的次数,利用梯度下降法循环优化w,w_grad是梯度。
def fit(self, X, y):
m_samples, n_features = X.shape
self.initialize_weights(n_features)
# 为X增加一列特征x1,x1 = 0
X = np.insert(X, 0, 1, axis=1)
y = np.reshape(y, (m_samples, 1))
# 梯度训练n_iterations轮
for i in range(self.n_iterations):
h_x = X.dot(self.w)
y_pred = sigmoid(h_x)
w_grad = X.T.dot(y_pred - y)
self.w = self.w - self.learning_rate * w_grad
# 预测函数,利用优化求得的w预测数据的分类。
def predict(self, X):
X = np.insert(X, 0, 1, axis=1)
h_x = X.dot(self.w)
y_pred = np.round(sigmoid(h_x))
return y_pred.astype(int) 3.3.1 运行结果

3.4 逻辑回归算法的优缺点
- 优点
- 训练速度快,分类的时候,计算量仅仅和特征的数目相关
- 简单易理解,模型可解释性非常好,从特征的权重可以看到不同的特征对最后结果的影响
- 适合二分类问题,不需要缩放输入特征
- 内存资源占用小,因为只需要存储各个维度的特征值
- 缺点
- 无法解决非线性问题
- 对多重共线性数据较为敏感
- 无法解决数据不平衡问题
- 本身无法筛选特征,需要结合其他模型来一起使用
3.5 机器学习面试高频题(与LR相关)
3.5.1 LR和SVM的联系和区别?
联系:
- 都是判别式模型
- 都是有监督的分类算法
- 如果不考虑核函数,都是线性分类算法
区别:
- LR可以输出概率,SVM不可以
- 损失函数不同,即分类机制不同
- SVM通过引入核函数解决非线性问题,LR则主要靠特征构造,必须组合交叉特征,特征离散化(原因:LR里每个样本点都要参与核计算,计算复杂度太高,故LR通常不用核函数)
3.5.2 LR 损失函数为什么用极大似然函数?
LR的目标是使每个样本的预测都有最大概率,即将所有样本预测后的概率相乘概率最大,这就是极大似然函数;
极大似然函数取对数即为对数损失函数,对数损失函数的训练求解参数比较快,更新速度也稳定。
3.5.3 LR为什么不用平方损失函数?
因为逻辑回归是分类算法,输出值y是离散的,而且是二值的,只有0或者1,用对数损失函数更直观;
平方损失函数是非凸的,不容易求解,很容易陷入局部最优,如果使用对数似然函数,可以证明它是关于(w,b)的高阶连续可导凸函数,可以方便通过一些凸优化算法求解,比如梯度下降法、牛顿法等。
3.5.4 LR为什么要对特征进行离散化?
- 稀疏向量做内积乘法运算速度快,计算结果方便存储,易于扩展;
- 离散化后的特征对异常数据有更强的鲁棒性;
- 特征离散化后模型更稳定;
- LR属于广义线性模型,表达能力有限,特征离散化为N个后,每个变量有自己的权重,相当于引入非线性,表达能力增强,加大拟合;
- 特征离散化后还可以做特征交叉,由
个变为
个,进一步引入非线性。
4. Naive Bayes(朴素贝叶斯)
贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。而朴素贝叶斯分类是贝叶斯分类中最简单,也是常见的一种分类方法。在开始讲解朴素贝叶斯分类算法之前,我们首先需要了解判别式学习算法和生成式学习算法以及它们之间的区别。
4.1 判别式学习算法和生成式学习算法
在机器学习中,对于有监督学习可以将其分为两类模型:判别式模型和生成式模型。简单地说,判别式模型是针对条件分布建模,而生成式模型则针对联合分布进行建模。这样听起来可能不好懂,我们这里举一个山羊和绵羊的例子来说明。
判别式模型:要确定一个羊是山羊还是绵羊,用判别式模型的方法是从历史数据中学习到模型,然后通过提取这只羊的特征来预测出这只羊是山羊的概率,是绵羊的概率。
生成式模型:是根据山羊的特征首先学习出一个山羊的模型,然后根据绵羊的特征学习出一个绵羊的模型,然后从这只羊中提取特征,放到山羊模型中看概率是多少,再放到绵羊模型中看概率是多少,哪个大就是哪个。
可以很清晰地看到差别,判别式模型是在寻找一个决策边界,通过该边界来将样本划分到对应类别。而生成式模型则不同,它学习了每个类别的边界,它包含了更多信息,可以用来生成样本。
4.2 贝叶斯公式
那么既然是朴素贝叶斯分类算法,它的核心算法又是什么呢?朴素贝叶斯算法的核心自然是贝叶斯公式:
在机器学习分类算法中,用以下形式可能会更加清晰明了:
我们最终求出P(类别|特征)的值即可!就相当于完成了我们的任务。
4.3 朴素贝叶斯算法的基本思想
- 如果要解决的是一个分类问题,那么我们的任务就是根据样本的特征来判断样本属于哪个类别。首先我们要对训练集中的样本进行统计,并计算各个类别数据所占的比例(先验概率):
- 接着计算各个类别下各个特征取到某值的概率(条件概率):
- 朴素贝叶斯算法假设各个特征相互独立,这样的话,对于测试集上的一个新样本来说,有以下等式成立:
- 给定测试集上的一个样本(也就是告知样本的各个特征的取值),我们可以计算出:
- 想要计算出后验概率P(类别y|特征),我们还需要计算出P(特征),但是任一样本的P(特征)在各个类别下的值是完全相同的,又因为我们的目的是找出样本属于哪个类别的概率最大,为了简化计算,分母部分的的P(特征)可以去掉。
4.4 拉普拉斯平滑
中有任何一部分的值为0,则整个式子的值为0。在对条件概率P(特征i的第k个可取值|类别y)进行建模时,发现它们很有可能为0,为了避免出现这种情况,可以引入拉普拉斯平滑。(为了解决零概率的问题,法国数学家拉普拉斯最早提出用加1的方法估计没有出现过的现象的概率,所以加法平滑也叫做拉普拉斯平滑)在建模过程中,假定每个特征的每个取值至少出现1次,这样:

4.5 朴素贝叶斯算法代码实现
#coding:utf-8
# 极大似然估计 朴素贝叶斯算法
import pandas as pd
import numpy as np
class NaiveBayes(object):
def getTrainSet(self):
dataSet = pd.read_csv('F://aaa.csv')
dataSetNP = np.array(dataSet) #将数据由dataframe类型转换为数组类型
trainData = dataSetNP[:,0:dataSetNP.shape[1]-1] #训练数据x1,x2
labels = dataSetNP[:,dataSetNP.shape[1]-1] #训练数据所对应的所属类型Y
return trainData, labels
def classify(self, trainData, labels, features):
#求labels中每个label的先验概率
labels = list(labels) #转换为list类型
labelset = set(labels)
P_y = {} #存入label的概率
for label in labelset:
P_y[label] = labels.count(label)/float(len(labels)) # p = count(y) / count(Y)
print(label,P_y[label])
#求label与feature同时发生的概率
P_xy = {}
for y in P_y.keys():
y_index = [i for i, label in enumerate(labels) if label == y] # labels中出现y值的所有数值的下标索引
for j in range(len(features)): # features[0] 在trainData[:,0]中出现的值的所有下标索引
x_index = [i for i, feature in enumerate(trainData[:,j]) if feature == features[j]]
xy_count = len(set(x_index) & set(y_index)) # set(x_index)&set(y_index)列出两个表相同的元素
pkey = str(features[j]) + '*' + str(y)
P_xy[pkey] = xy_count / float(len(labels))
print(pkey,P_xy[pkey])
#求条件概率
P = {}
for y in P_y.keys():
for x in features:
pkey = str(x) + '|' + str(y)
P[pkey] = P_xy[str(x)+'*'+str(y)] / float(P_y[y]) #P[X1/Y] = P[X1Y]/P[Y]
print(pkey,P[pkey])
#求[2,'S']所属类别
F = {} #[2,'S']属于各个类别的概率
for y in P_y:
F[y] = P_y[y]
for x in features:
F[y] = F[y]*P[str(x)+'|'+str(y)] #P[y/X] = P[X/y]*P[y]/P[X],分母相等,比较分子即可,所以有F=P[X/y]*P[y]=P[x1/Y]*P[x2/Y]*P[y]
print(str(x),str(y),F[y])
features_label = max(F, key=F.get) #概率最大值对应的类别
return features_label
if __name__ == '__main__':
nb = NaiveBayes()
# 训练数据
trainData, labels = nb.getTrainSet()
# x1,x2
features = [8]
# 该特征应属于哪一类
result = nb.classify(trainData, labels, features)
print(features,'属于',result) 4.5.1 运行结果

4.6 朴素贝叶斯算法应用实例
某个医院早上收了6个门诊病人,如下表:
| 症状 | 职业 | 疾病 |
|---|---|---|
| 打喷嚏 | 护士 | 感冒 |
| 打喷嚏 | 农夫 | 没患感冒 |
| 头痛 | 建筑工人 | 没患感冒 |
| 头痛 | 建筑工人 | 感冒 |
| 打喷嚏 | 教师 | 感冒 |
| 头痛 | 教师 | 没患感冒 |
现在又来了第七个病人,是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大?
- 根据贝叶斯公式可得:
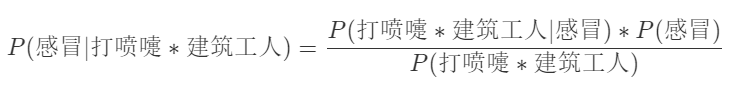
- 假定“打喷嚏”和“建筑工人”这两个特征是相互独立的,因此,上面的等式就变成了:

- 按照以上公式进行统计、计算:

- 那他没患上感冒的概率为0.33,我们可以通过以下式子进行验证:

4.7 朴素贝叶斯算法的优缺点
优点
- 所估计的参数少,有稳定的分类效率
- 对小规模的数据表现良好,能处理多分类任务,假设条件概率计算是彼此独立的,因此适合增量式训练,尤其是数据量超出内存时,可以一批批的去增量训练
- 属于生成式模型,收敛速度比判别式模型要快
- 对缺失数据不太敏感,算法也比较简单,常用于文本分类
- 天然可以处理多分类问题
缺点
- 理论上,朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此,这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立,这个假设在实际应用中往往是不成立的,在属性个数比较多或者属性之间相关性较大时,分类效果不好。而在属性相关性较小时,朴素贝叶斯性能最为良好。对于这一点,有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进
- 需要知道先验概率,且先验概率很多时候取决于假设,假设的模型可以有很多种,因此在某些时候会由于假设的先验模型的原因导致预测效果不佳
- 由于我们是通过先验和数据来决定后验的概率从而决定分类,所以分类决策存在一定的错误率
- 对输入数据的表达形式比较敏感
适用场景
- 支持大规模数据,并且支持分布式实现;
- 特征维度可以很高;
- 可以处理数值型特征和类别型特征。
4.8 机器学习面试高频题(与朴素贝叶斯相关)
朴素贝叶斯中“朴素”是什么意思?
朴素的含义为:假设各个特征之间相互独立。
参考文献
- 李航 ---《统计学习方法》
- 周志华 --- 《机器学习》
- Peter Harrington --- 《Machine Learning in Action》
- 知乎 --- 《机器学习中的判别式模型和生成式模型》
 查看14道真题和解析
查看14道真题和解析