分类网络

ResNeXt

ResNeXt是在ResNet之后进一步提出的分类网络,看它的名字就知道了.ResNeXt,可以看成ResNet和Next,果然写文章的都是一群取名鬼才.
论文:Aggregated Residual Transformations for Deep Neural Networks
代码

思路来源

作者认为,尽管增大网络的深度和width(指features maps的个数)可能提高模型的准确率,但与此同时带来的是网络的复杂度不断增大.
作者发现,增加网络内部transformation的个数,能够在不增大模型复杂度的前提下,提高模型的精度.增加网络内部transformation的个数即通过增加多个分支来实现.

多分支的通用表达

作者给出了一个表达式,用来囊括表达各种多分支的结构.

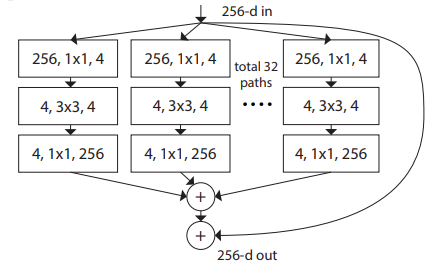
如图中所示,共有 $C(C=32)$C(C=32)个分支,每个分支记为 $T_i$Ti​,对应一种变换(Transformation),每个变换里可能有不同的结构.输入经过每个分支的变换之后,再加和在一起,因此多个分支的变换表达式为:
$F\left(x\right)=\sum _{i=1}^C{T}_i\left(x\right)$F(x)=i=1∑C​Ti​(x)
另外还有一条直连结构(shortcut),因此整个模块的表达式为:
$y=x+\sum _{i=1}^C{T}_i\left(x\right)$y=x+i=1∑C​Ti​(x)

多分支模块的设计与等效表达

本着大道至简的原则,作者认为去除"五花八门"的分支(如下图),转而采用同样的分支结构,这样也可以提高模型的鲁棒性,避免在某个数据集上过拟合.

作者提出的分支模块如下图所示,每个分支具有相同的结构.

• 先用 $1\ast 1$1∗1的卷积降维
• 进行 $3\ast 3$3∗3的卷积
• 再用 $1\ast 1$1∗1的卷积升维

下面对该模块进行等效变换.
记3*3卷积的输出为: $h_{b,i}^3$hb,i3​,其中3表示3*3的卷积, $b$b表示分支的编号( $b=1,2,...,32$b=1,2,...,32), $i$i表示特征图channel的编号( $i=1,2,3,4$i=1,2,3,4).所有分支3*3卷积之后共计有 $32\ast 4=128$32∗4=128个 $h$h.
$h_{b,j}^1$hb,j1​ 表示1*1卷积之后的输出, $j=1,2,...,256$j=1,2,...,256.
某个分支1*1卷积后的一个输出可表示为:
$h_{b,j}^1=\sum _{i=1}^4{w}_{b,i,j}{h}_{b,i}^3$hb,j1​=i=1∑4​wb,i,j​hb,i3​
将所有分支的结果求和,得到所有分支的汇总输出:

$\begin{array}{cc}{\displaystyle y_j}& {\displaystyle =\sum _{b=1}^{32}{h}_{b,j}^1}\\ {\displaystyle }& {\displaystyle =\sum _{b=1}^{32}\sum _{i=1}^4{w}_{b,i,j}{h}_{b,i}^3}\end{array}$yj​​=b=1∑32​hb,j1​=b=1∑32​i=1∑4​wb,i,j​hb,i3​​
该表达式的本质就是,将每一个分支的每一个通道乘上一个系数,再求和!
也就是说,在计算的时候,其实和分支关系不大.如果对每个分支的每个通道进行统一的编号,编号方式为 $k=(b-1)\ast 4+i$k=(b−1)∗4+i,那么上式可改写成:
$y_j=\sum _{k=1}^{128}{w}_{k,j}{h}_k^3$yj​=k=1∑128​wk,j​hk3​
根据这个式子,就可以把结构等效成下面这个结构了.

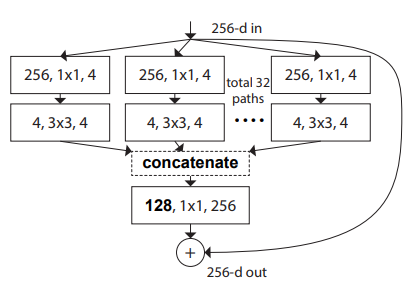
• 先将每个分支3*3卷积的结果堆叠在一起,相当于根据分支对通道进行统一的编号.
• 再将堆叠的结果进行1*1的卷积计算.

concat之后的输出为:
$h_k^3,k=1,2,...,128$hk3​,k=1,2,...,128
1*1卷积之后的结果为:
$y_j=\sum _{k=1}^{128}{w}_{k,j}{h}_k^3$yj​=k=1∑128​wk,j​hk3​
和第一种结构的式子完全等价!

接下来再进行一次变换.

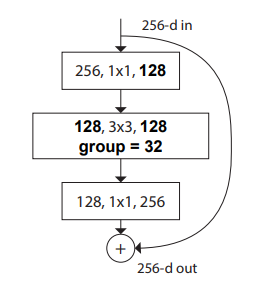
解释:

• 每个分支的1*1的卷积可以组合在一起计算,计算之后每个分支分4个channels.由于每一个输出channel是依据输入channel进行全连接计算的,因此每个输出Channel之间是独立的.所以分开计算和一起计算等价.
• 再看3*3的卷积,每个分支是在各自的4个channel中计算,正好就是Group Convolution(挖个坑,接下来的博客会专门总结各种卷积方式)的计算方式.

对比ResNet

ResNet的BottleNeck结构:

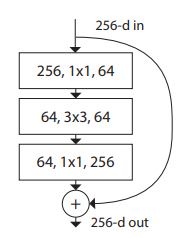
ResNeXt的BottleNeck结构:

乍一看,两个也长得差不多,主要有两点变化:

• 通道数增加
• 普通卷积换成了分组卷积

二者参数量对比:

二者参数量相当.

但是ResNeXt增大了通道数和分支数,相当于增大了网络的宽度(width),提高了网络的表达能力(Model Capacity).所以在保持模型复杂度的前提下,提高了模型的精度.

小结

再回头看,其实就是把普通卷积换成了分组卷积 = = .但作者能够关联到网络分支,网络结构的表达能力,并给出一系列的论证,并做了大量的实验来验证想法,或许这就是艺术吧!